The Softmax Function is Linear

I asked my Twitter followers if they knew that the softmax function is linear. The result was disbelief.

In this post, I’ll give a short proof that the softmax function is a linear map from real vectors of $d$ dimensions ($\mathbb{R}^d$) to probability distributions over $d$ variables ($\Delta_d)$. I will assume some basic understanding of linear algebra. We will begin by defining both the softmax function and linear maps.

\[\mathrm{softmax}(\vec{x})=\frac{\exp\vec{x}}{\sum_i\exp x_i}\]

Linear map: For two real vector spaces $V$ and $W$ with vector addition operators $\oplus_V$ and $\oplus_W$ and scalar multiplication operators $\otimes_V$ and $\otimes_W$, a map $f:V\to W$ is linear if for all vectors $\vec u,\vec v\in V$ we have $f(\vec u\oplus_V\vec v)=f(\vec u)\oplus_Wf(\vec v)$ (a property called additivity), and for any scalar $\lambda\in\mathbb{R}$ we have $\lambda\otimes_Wf(\vec u) = f(\lambda\otimes_V\vec u)$ (a property called homogeneity).

To prove that the softmax funtion is a linear map, we will therefore need to show

$\mathbb{R}^d$ and $\Delta_d$ are real vector spaces.
The softmax function satisfies additivity.
The softmax function satisfies homogeneity.

$\mathbb{R}^d$ and $\Delta_d$ are real vector spaces

$\mathbb{R}^d$ is a canonical vector space, where vector addition is defined as \[(u_1,u_2,\ldots,u_d)\oplus_{\mathbb{R}^d}(v_1,v_2,\ldots,v_d)=(u_1+v_1, u_2+v_2, \ldots, u_d+v_d)\] and scalar multiplication as \[\lambda\otimes_{\mathbb{R}^d}(u_1,u_2,\ldots,u_d)=(\lambda u_1,\lambda u_2, \ldots,\lambda u_d).\] For convenience, we will denote $\vec{u}\oplus_{\mathbb{R}^d}\vec{v}$ as $\vec{u}+\vec{v}$, and $\lambda\otimes_{\mathbb{R}^d}\vec{u}$ as $\lambda\vec{u}$, as this is common notation for vector arithmetic in $\mathbb{R}^d$.

It is an underappreciated fact that $\Delta_d$ is also a real vector space. In particular, the elements of $\Delta_d$ are $d$-dimensional tuples of positive reals whose entries sum to 1 \[\Delta_d=\left\{\vec{u}\in(0,\infty)^d \mid \sum_{i=1}^du_i=1\right\}.\]

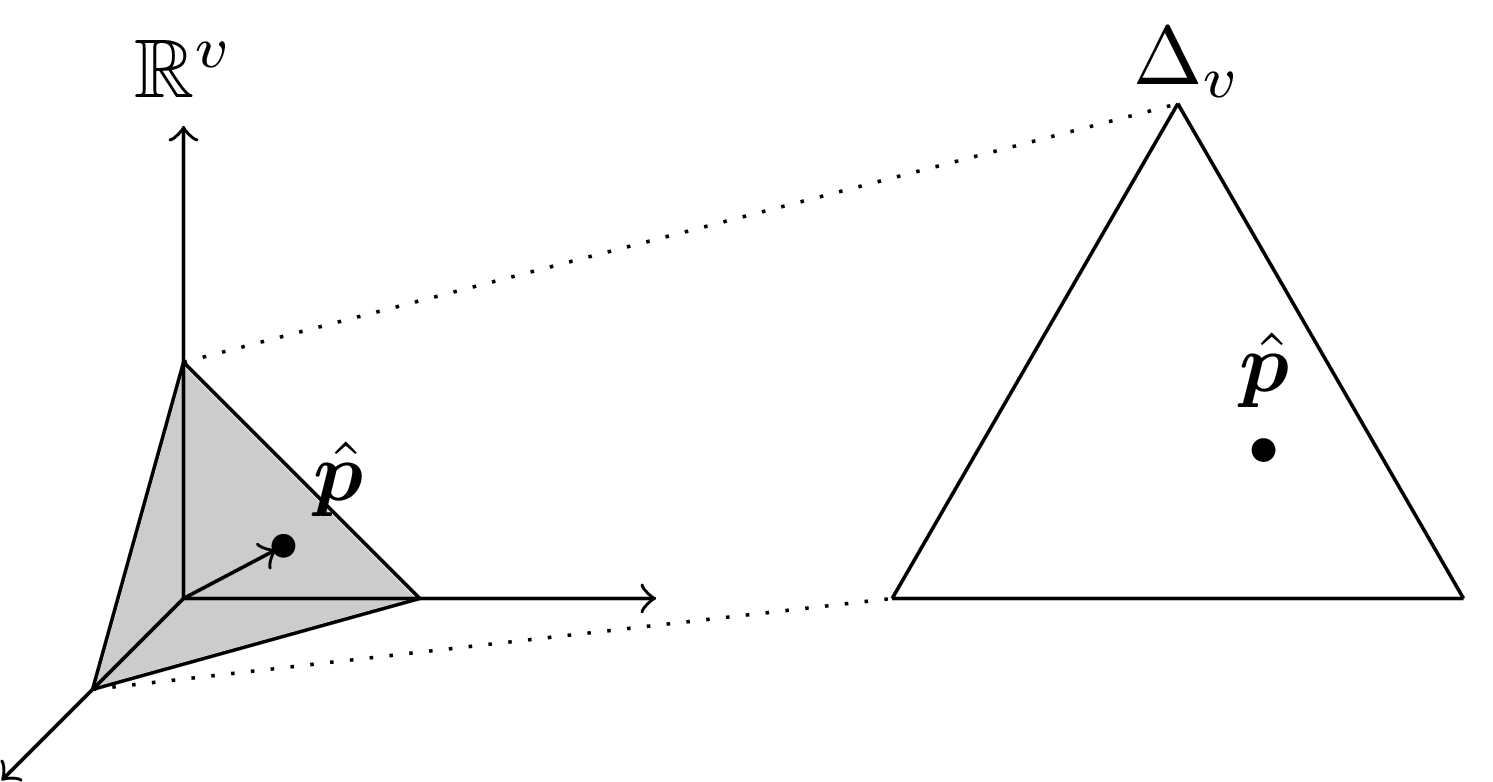
\Delta_d is also known as the d-simplex. Here we visualize the 3-simplex. Vectors like the one shown above (\hat{p}) that lie on the 3-simplex are valid probability distributions over 3 items. — $\Delta_d$ is also known as the $d$-simplex. Here we visualize the 3-simplex. Vectors like the one shown above ($\hat{p}$) that lie on the 3-simplex are valid probability distributions over 3 items.

To add two vectors $u,v\in\Delta_d$, we multiply them element-wise and divide by their sum \[\vec{u}\oplus_{\Delta_d}\vec{v}=\frac{\vec{u}\odot\vec{v}}{\sum_{i=1}^du_iv_i}.\] To multiply a vector $\vec{u}\in\Delta_d$ by a scalar $\lambda\in\mathbb{R}$, we exponentiate elements by $\lambda$ and renormalize \[ \lambda\otimes_{\Delta_d}(u_1,u_2,\ldots,u_d) =\frac{(u_1^\lambda,u_2^\lambda,\ldots,u_d^\lambda)}{\sum_{i=1}^du_i^\lambda}. \] For convenience, we will denote these operations as $\oplus$ and $\otimes$, dropping the subscript.

Additivity

Our goal is to show that for all vectors $\vec u,\vec v\in \mathbb{R}^d$ \[\mathrm{softmax}(\vec u+\vec v)=\mathrm{softmax}(\vec u)\oplus\mathrm{softmax}(\vec v).\] Jumping right in, \[\begin{aligned} \mathrm{softmax}(\vec u + \vec v) &= \frac{\exp(\vec u+\vec v)}{\sum_{i=1}^d\exp(u_i+v_i)} & \text{softmax defn}\\ &= \frac{\exp(\vec{u})\odot\exp(\vec{v})}{\sum_{i=1}^d\exp(u_i)\exp(v_i)} & \text{exp identity} \\ &= \frac{\exp(\vec{u})}{\sum_{i=1}^d\exp(u_i)}\oplus\frac{\exp(\vec{v})}{\sum_{i=1}^d\exp(v_i)} & \oplus\text{ defn} \\ &= \mathrm{softmax}(\vec{u})\oplus\mathrm{softmax}(\vec{v}) & \text{softmax defn.} \end{aligned}\]

Homogeneity

Our goal is to show that for all vectors $\vec u\in \mathbb{R}^d$ and $\lambda\in\mathbb{R}$, \[\lambda\otimes\mathrm{softmax}(\vec u)=\mathrm{softmax}(\lambda\vec u).\] By a similar derivation, \[\begin{aligned} \lambda\otimes\mathrm{softmax}(\vec u) &= \lambda\otimes\frac{\exp(\vec{u})}{\sum_{i=1}^d\exp(u_i)} & \text{softmax defn}\\ &= \frac{\exp(\vec{u})^\lambda}{\sum_{i=1}^d\exp(u_i)^\lambda} & \text{$\otimes$ defn}\\ &= \frac{\exp(\lambda\vec{u})}{\sum_{i=1}^d\exp(\lambda\vec{u})_i} & \text{exp identity}\\ &=\mathrm{softmax}(\lambda\vec u) & \text{softmax defn.} \end{aligned}\]

Conclusion

Having shown additivity and homogeneity we have proven that the softmax function is a linear map! Why is this important? For one, this knowledge can give us intuition for how the softmax bottleneck limits the possible outputs of language models.

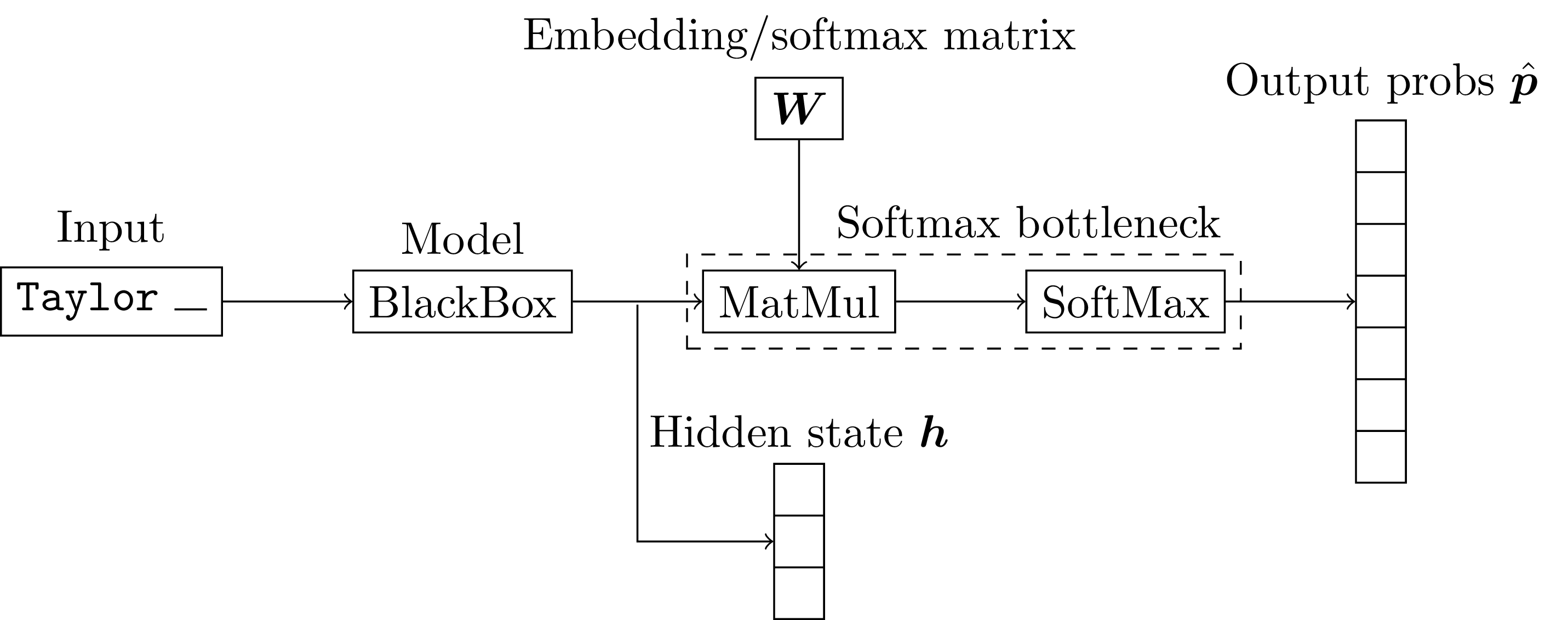
A linear map W composed with the softmax function projects language model hidden states to probability distributions. — A linear map $W$ composed with the softmax function projects language model hidden states to probability distributions.

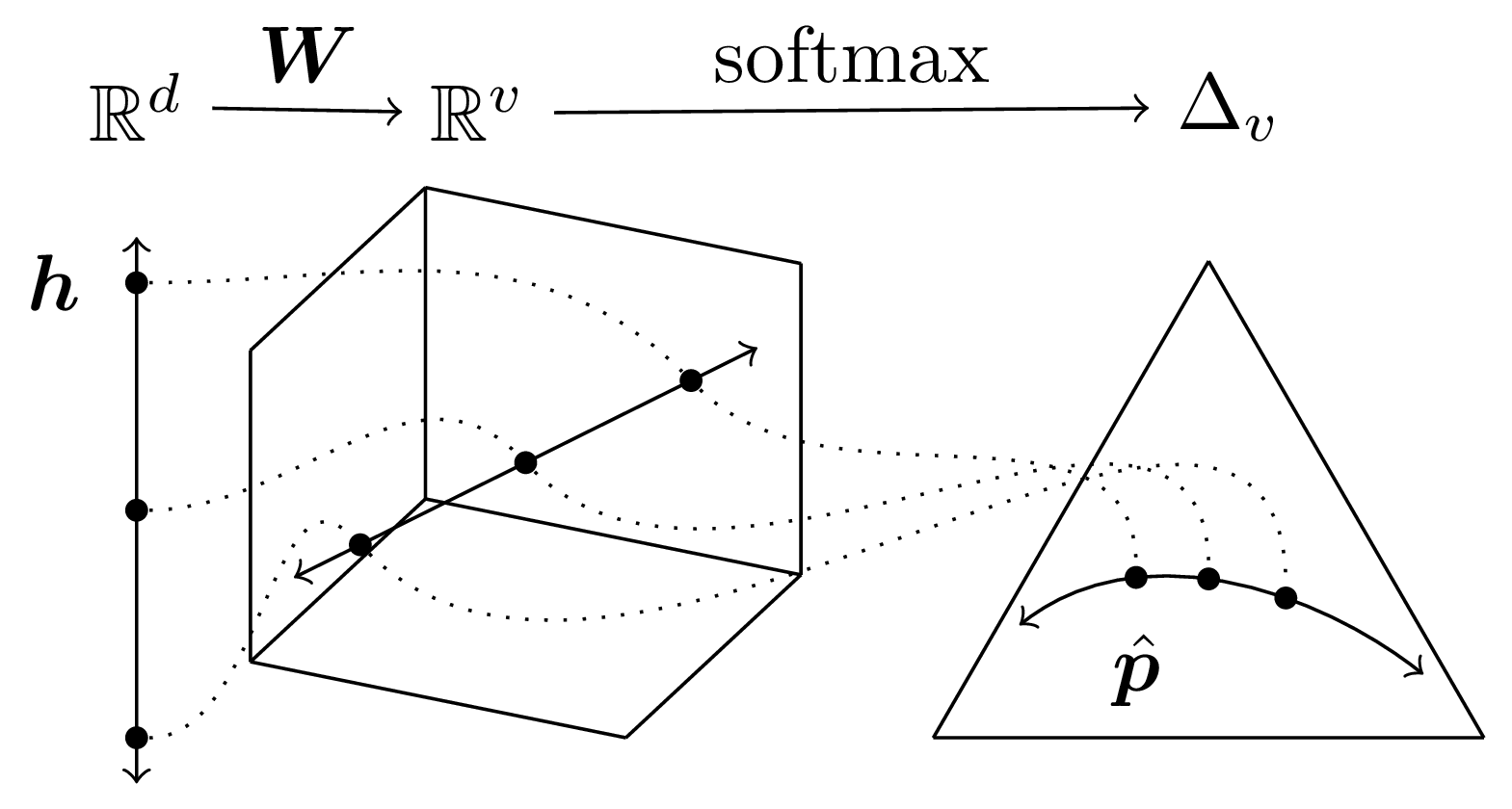
Because the low-rank projection W and the softmax function are linear, their composed image is a strict linear subspace of \Delta_v the vector space of distributions over a vocabulary of size v. — Because the low-rank projection $W$ and the softmax function are linear, their composed image is a strict linear subspace of $\Delta_v$ the vector space of distributions over a vocabulary of size $v$.

In my recent paper, we use this knowledge to develop a better generation algorithm for language models that directly addresses this source of model errors.

Thank you for reading! For questions and comments, you are welcome to email me at mattbnfin@gmail.com.

\(\mathbb{R}^d\) and \(\Delta_d\) are real vector spaces

Additivity

Homogeneity

Conclusion